SVM

Support Vector Machine

Theory

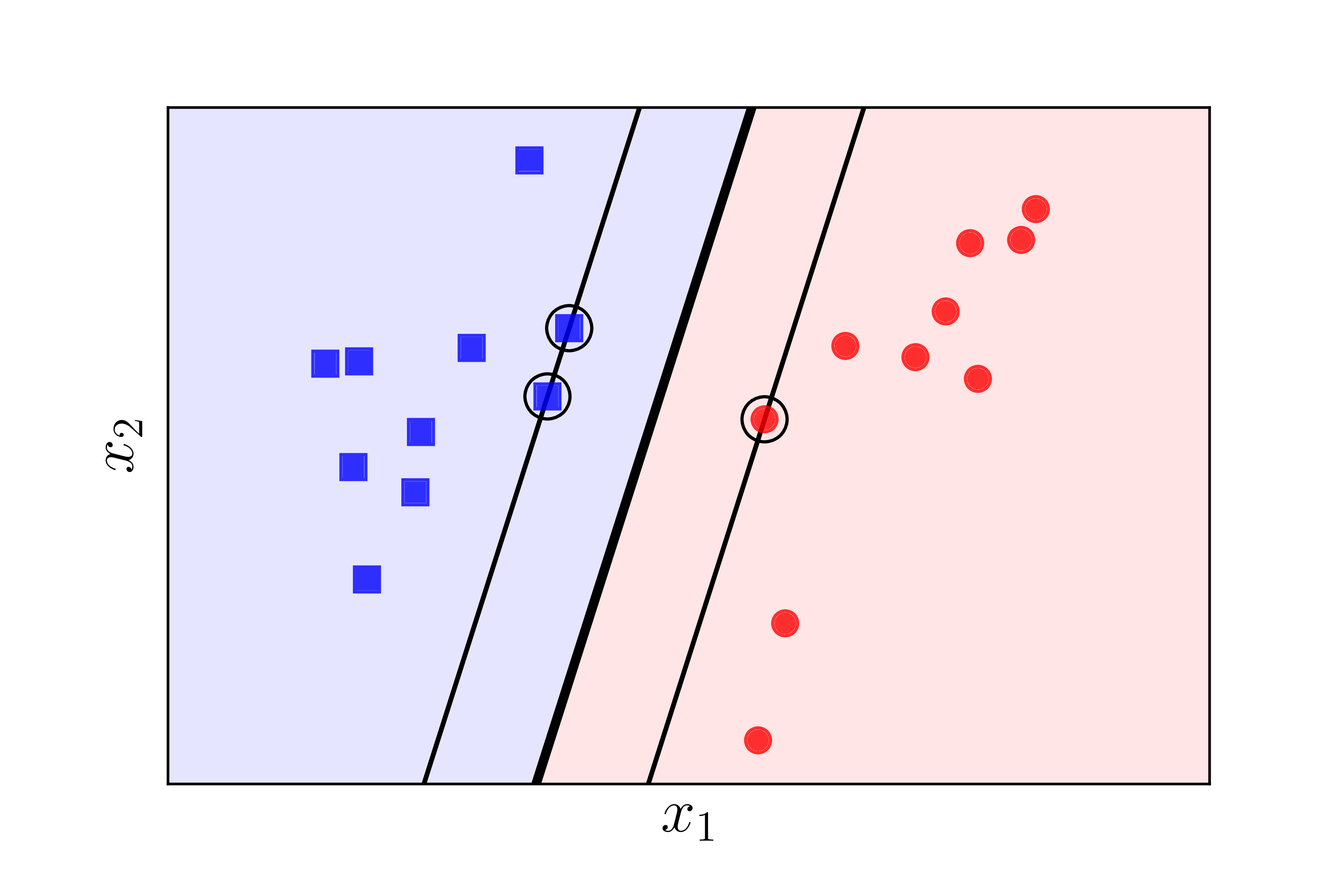
Support Vector Machine (SVM) is a powerful classifier that finds the optimal hyperplane maximizing the margin between two classes. Only support vectors (points on the margin) matter for defining the decision boundary.

Visualization

Mathematical Formulation

Hard Margin SVM:
minimize ½||w||²
subject to yᵢ(w·xᵢ + b) ≥ 1

Margin: 1/||w||

Decision Function:
sign(w·x + b)

Support Vectors:
Points where yᵢ(w·xᵢ + b) = 1

Code Example

from sklearn import svm
from sklearn.datasets import make_blobs
import numpy as np

# Generate linearly separable data
X, y = make_blobs(n_samples=100, n_features=2, 
                  centers=2, random_state=42)
y = np.where(y == 0, -1, 1)

# Train SVM
clf = svm.SVC(kernel='linear', C=1000)
clf.fit(X, y)

# Get support vectors
support_vectors = clf.support_vectors_
print(f"Number of support vectors: {len(support_vectors)}")
print(f"Support vector indices: {clf.support_}")

# Calculate margin
w = clf.coef_[0]
margin = 2 / np.linalg.norm(w)
print(f"Margin width: {margin:.4f}")

# Predict
predictions = clf.predict(X)
accuracy = np.mean(predictions == y)
print(f"Accuracy: {accuracy:.3f}")

Duality

Soft Margin SVM