Recommender Systems

Matrix Factorization Collaborative Filtering

Theory

Matrix Factorization decomposes the user-item rating matrix into lower-dimensional latent factor matrices, capturing hidden patterns in preferences. It handles sparse data well and scales to large datasets.

Visualization

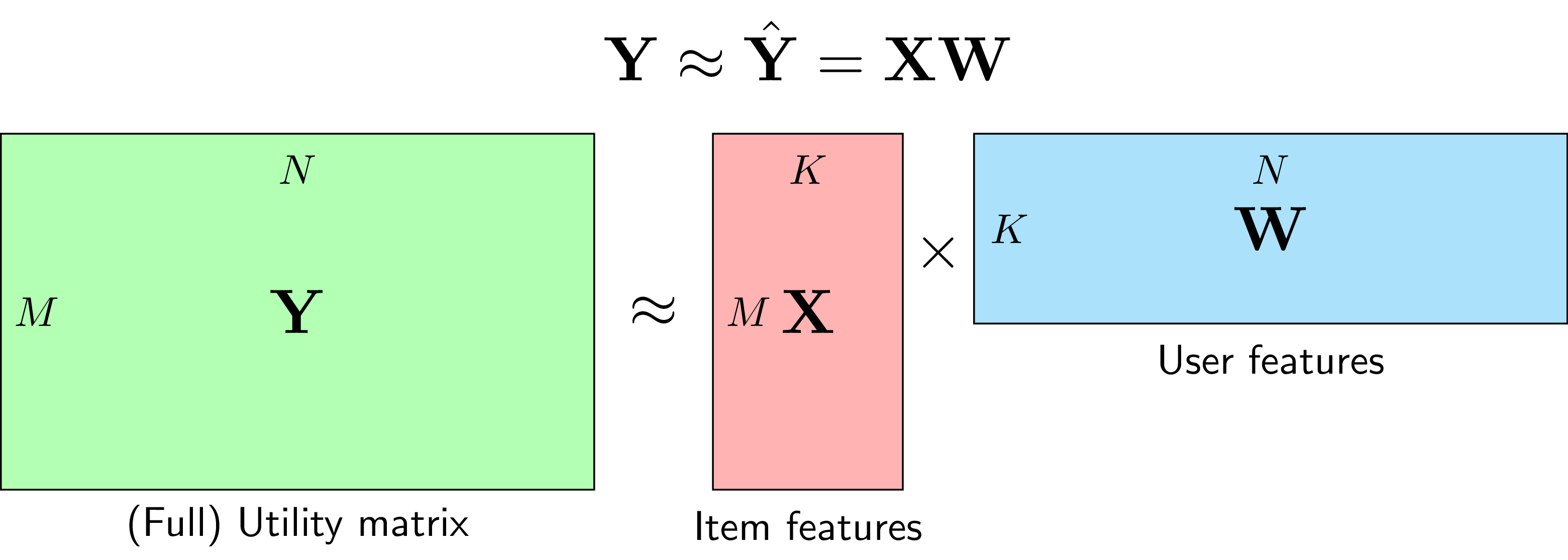
Mathematical Formulation

Formulation:
R ≈ P × Qᵀ

R: m×n rating matrix
P: m×k user factors
Q: n×k item factors

Optimization (SGD):
minimize Σ(rᵤᵢ - pᵤ·qᵢ)² + λ(||pᵤ||² + ||qᵢ||²)

Code Example

import numpy as np
from scipy.sparse.linalg import svds

# Sample ratings
R = np.array([
    [5, 4, 0, 0, 3],
    [4, 0, 0, 5, 4],
    [0, 5, 4, 0, 5],
    [3, 0, 5, 4, 0]
])

print("Original Rating Matrix:")
print(R)

# Matrix Factorization using SVD
n_factors = 2

# Center ratings
R_mean = R[R > 0].mean()
R_centered = R.copy()
R_centered[R > 0] -= R_mean

# SVD
U, sigma, Vt = svds(R_centered, k=n_factors)

# Reconstruct
R_pred = U @ np.diag(sigma) @ Vt + R_mean
R_pred = np.clip(R_pred, 1, 5)

print("\nPredicted Ratings:")
print(R_pred.round(2))

# Alternative: Gradient Descent
def matrix_factorization_gd(R, k=2, steps=5000, 
                           alpha=0.002, beta=0.02):
    """Train with gradient descent"""
    m, n = R.shape
    P = np.random.rand(m, k)
    Q = np.random.rand(n, k)
    
    for step in range(steps):
        for i in range(m):
            for j in range(n):
                if R[i, j] > 0:
                    eij = R[i, j] - np.dot(P[i], Q[j])
                    P[i] += alpha * (2 * eij * Q[j] - beta * P[i])
                    Q[j] += alpha * (2 * eij * P[i] - beta * Q[j])
    
    return P, Q.T

P, Qt = matrix_factorization_gd(R)
R_pred_gd = P @ Qt
print("\nGradient Descent Predictions:")
print(R_pred_gd.round(2))

Collaborative Filtering

SVD