Optimization

Gradient Descent (1/2)

Theory

Gradient Descent is an iterative optimization algorithm for finding the minimum of a function. It's the foundation for training many machine learning models. The algorithm starts with random parameters and iteratively moves in the direction of steepest descent (negative gradient).

Visualization

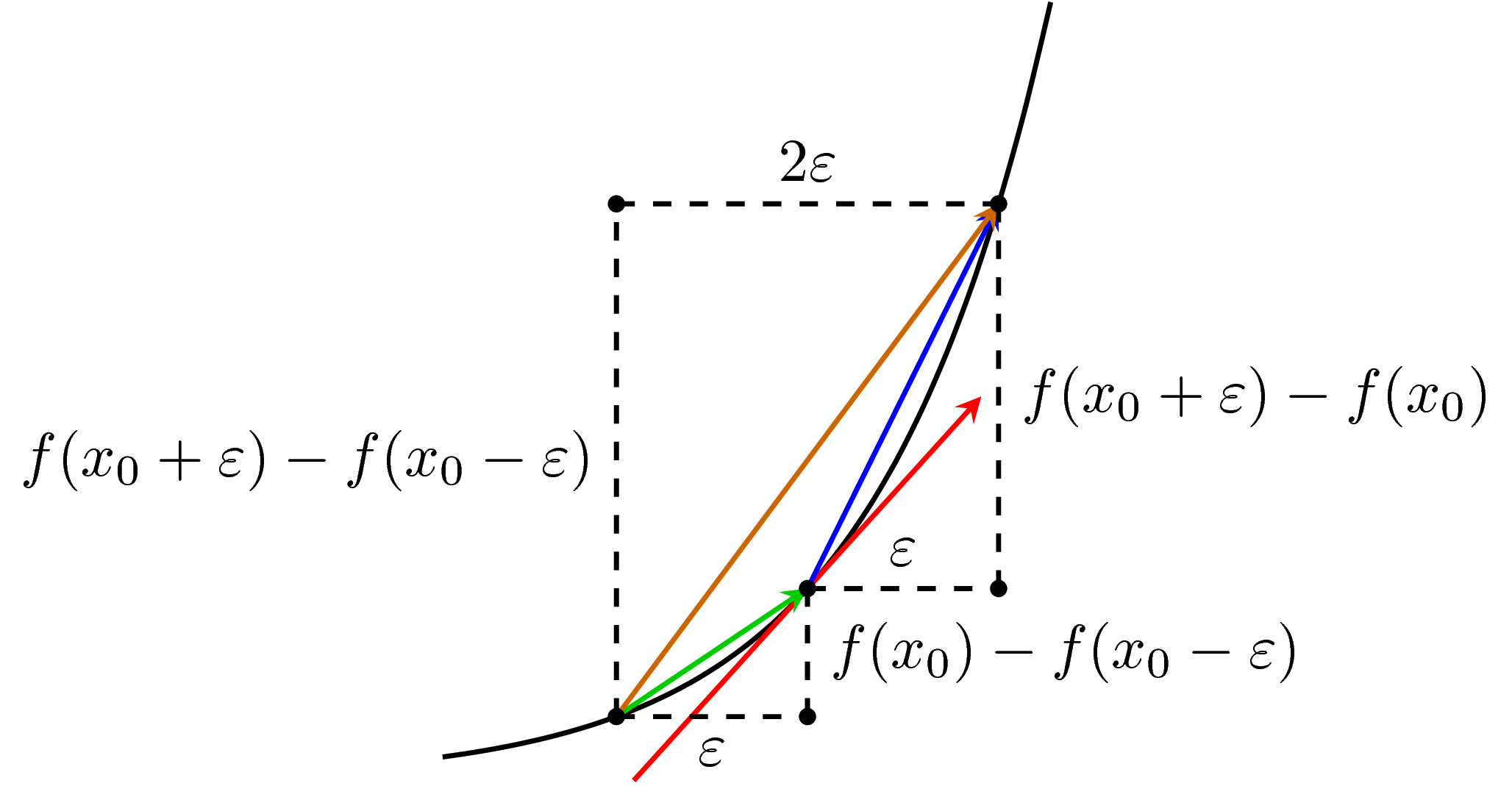
Mathematical Formulation

Update Rule:
θ = θ - α · ∇J(θ)

Where:
• θ = parameters
• α = learning rate (step size)
• ∇J(θ) = gradient of cost function

Code Example

import numpy as np

def cost_function(theta, X, y):
    """Mean Squared Error"""
    m = len(y)
    predictions = X.dot(theta)
    return (1/(2*m)) * np.sum((predictions - y)**2)

def gradient_descent(X, y, theta, alpha, iterations):
    """Basic gradient descent implementation"""
    m = len(y)
    cost_history = []
    
    for i in range(iterations):
        # Calculate predictions
        predictions = X.dot(theta)
        
        # Calculate gradient
        gradient = (1/m) * X.T.dot(predictions - y)
        
        # Update parameters
        theta = theta - alpha * gradient
        
        # Track cost
        cost = cost_function(theta, X, y)
        cost_history.append(cost)
    
    return theta, cost_history

# Example usage
X = np.array([[1, 1], [1, 2], [1, 3], [1, 4]])
y = np.array([2, 4, 5, 4])
theta = np.zeros(2)

theta_final, costs = gradient_descent(
    X, y, theta, alpha=0.01, iterations=1000
)

print(f"Final parameters: {theta_final}")
print(f"Final cost: {costs[-1]:.4f}")

K-nearest Neighbors

Gradient Descent (2/2)