Optimization

Duality

Theory

Duality is a powerful concept in optimization. Every optimization problem (primal) has an associated dual problem. For convex problems, solving either gives the same optimal value. SVMs are solved via their dual formulation, enabling the kernel trick.

Visualization

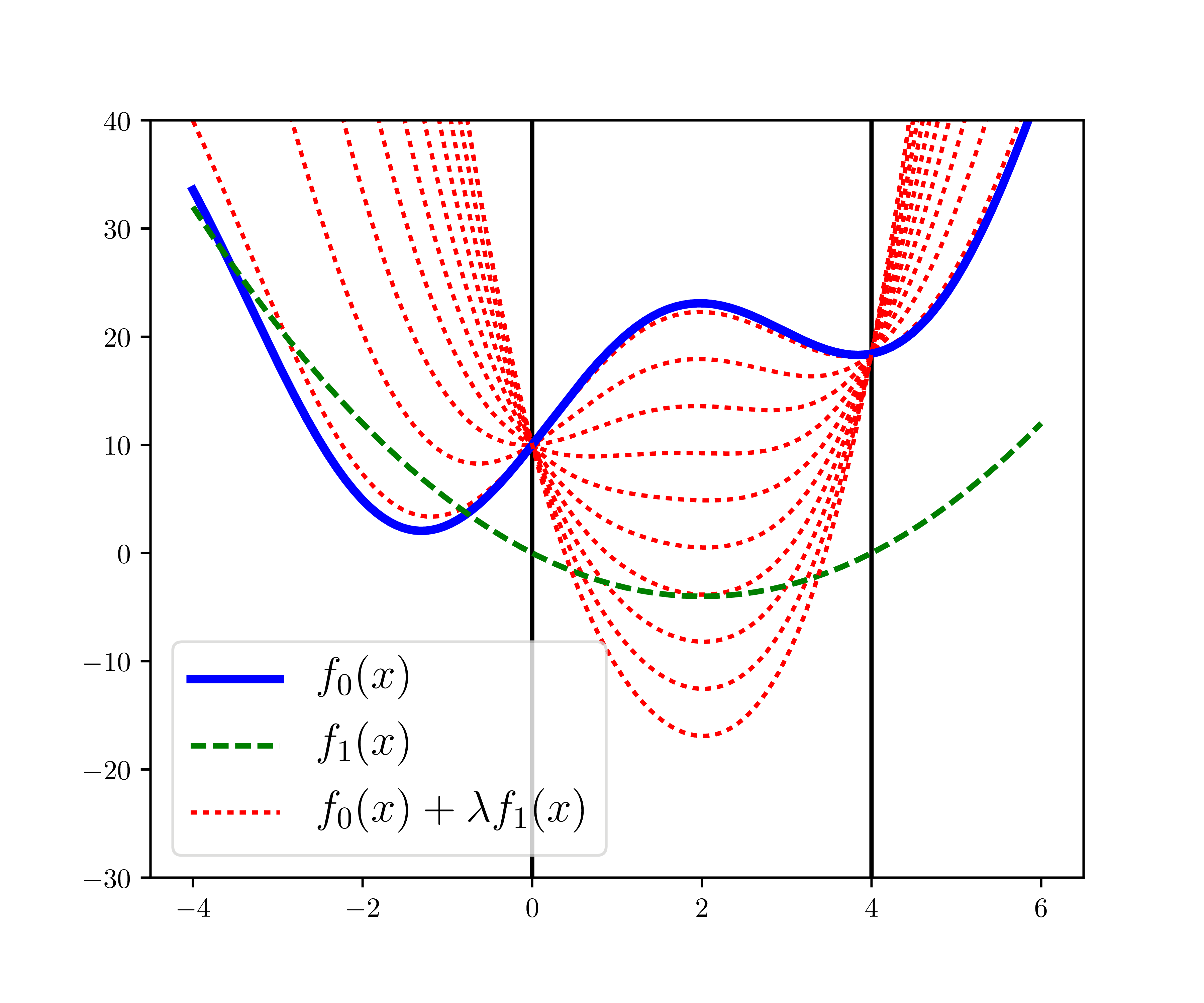
Mathematical Formulation

Lagrangian:
L(x, λ, ν) = f(x) + Σλᵢgᵢ(x) + Σνⱼhⱼ(x)

Dual Function:
g(λ, ν) = infₓ L(x, λ, ν)

Key Results:
• Weak Duality: d* ≤ p*
• Strong Duality: d* = p* (for convex)
• KKT Conditions: Necessary & sufficient for optimality

Code Example

import numpy as np
from scipy.optimize import minimize

# Example: Linear Program and its Dual
# Primal: min c^T x s.t. Ax <= b, x >= 0
# Dual:   max b^T λ s.t. A^T λ <= c, λ >= 0

c = np.array([1, 2])
A = np.array([[1, 1], [2, 1]])
b = np.array([4, 5])

# Solve primal
def primal_obj(x):
    return c @ x

def primal_cons(x):
    return b - A @ x

primal_result = minimize(
    primal_obj, x0=[0, 0],
    bounds=[(0, None), (0, None)],
    constraints={'type': 'ineq', 'fun': primal_cons}
)

# Solve dual
def dual_obj(lam):
    return -(b @ lam)

def dual_cons(lam):
    return c - A.T @ lam

dual_result = minimize(
    dual_obj, x0=[0, 0],
    bounds=[(0, None), (0, None)],
    constraints={'type': 'ineq', 'fun': dual_cons}
)

print(f"Primal optimal: {primal_result.fun:.4f}")
print(f"Dual optimal: {-dual_result.fun:.4f}")
print(f"Duality gap: {abs(primal_result.fun + dual_result.fun):.6f}")

Convex Optimization

Support Vector Machine