Optimization

Convex Sets and Convex Functions

Theory

Convex optimization is fundamental to many machine learning algorithms. Understanding convex sets and functions helps ensure we can find global optima. A key property: any local minimum of a convex function is also a global minimum.

Visualization

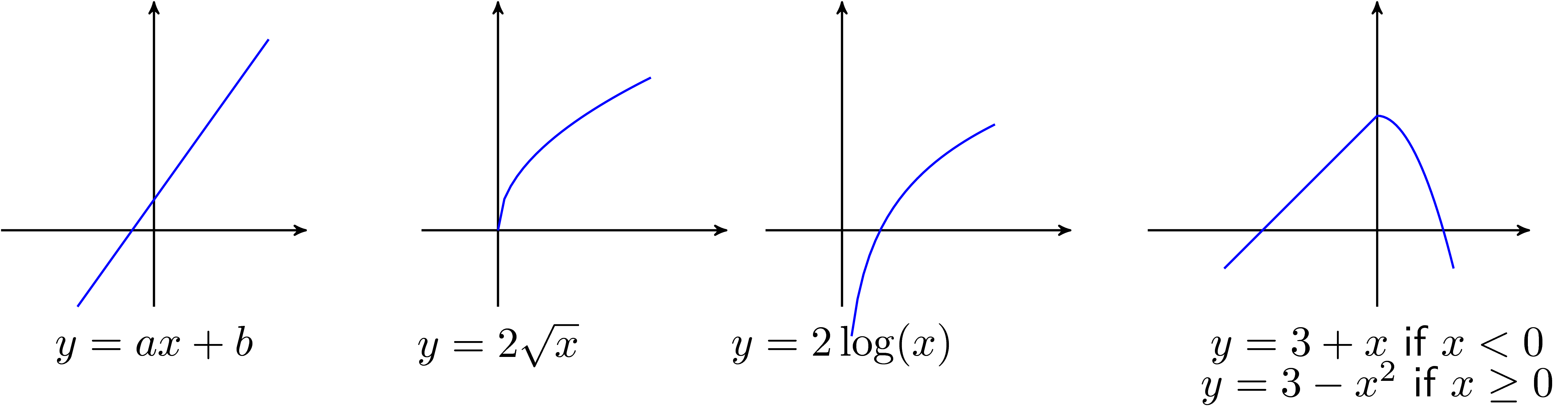
Mathematical Formulation

Convex Set:
θx + (1-θ)y ∈ C for all x,y ∈ C and θ ∈ [0,1]

Convex Function:
f(θx + (1-θ)y) ≤ θf(x) + (1-θ)f(y)

Examples:
• Convex: x², |x|, eˣ, max(x₁,...,xₙ)
• Not convex: x³, sin(x), x⁴-x²

Code Example

import numpy as np
import matplotlib.pyplot as plt

# Convex function: f(x) = x^2
x = np.linspace(-5, 5, 100)
y_convex = x**2

# Non-convex: f(x) = x^3 - 3x
y_nonconvex = x**3 - 3*x

# Check convexity numerically
def is_convex(f, x_range, n_samples=1000):
    """Numerical convexity check"""
    points = np.random.uniform(x_range[0], x_range[1], 
                              (n_samples, 2))
    theta = np.random.uniform(0, 1, n_samples)
    
    x1, x2 = points[:, 0], points[:, 1]
    interpolated = theta * x1 + (1 - theta) * x2
    
    # Check convexity condition
    left = f(interpolated)
    right = theta * f(x1) + (1 - theta) * f(x2)
    
    return np.all(left <= right + 1e-6)

# Test
f_convex = lambda x: x**2
f_nonconvex = lambda x: x**3 - 3*x

print(f"x² is convex: {is_convex(f_convex, [-5, 5])}")
print(f"x³-3x is convex: {is_convex(f_nonconvex, [-5, 5])}")

Overfitting

Convex Optimization