Optimization

Convex Optimization Problems

Theory

A convex optimization problem has a convex objective function and convex constraints. These problems can be solved efficiently with guaranteed global optimality. Many ML algorithms are formulated as convex optimization problems.

Visualization

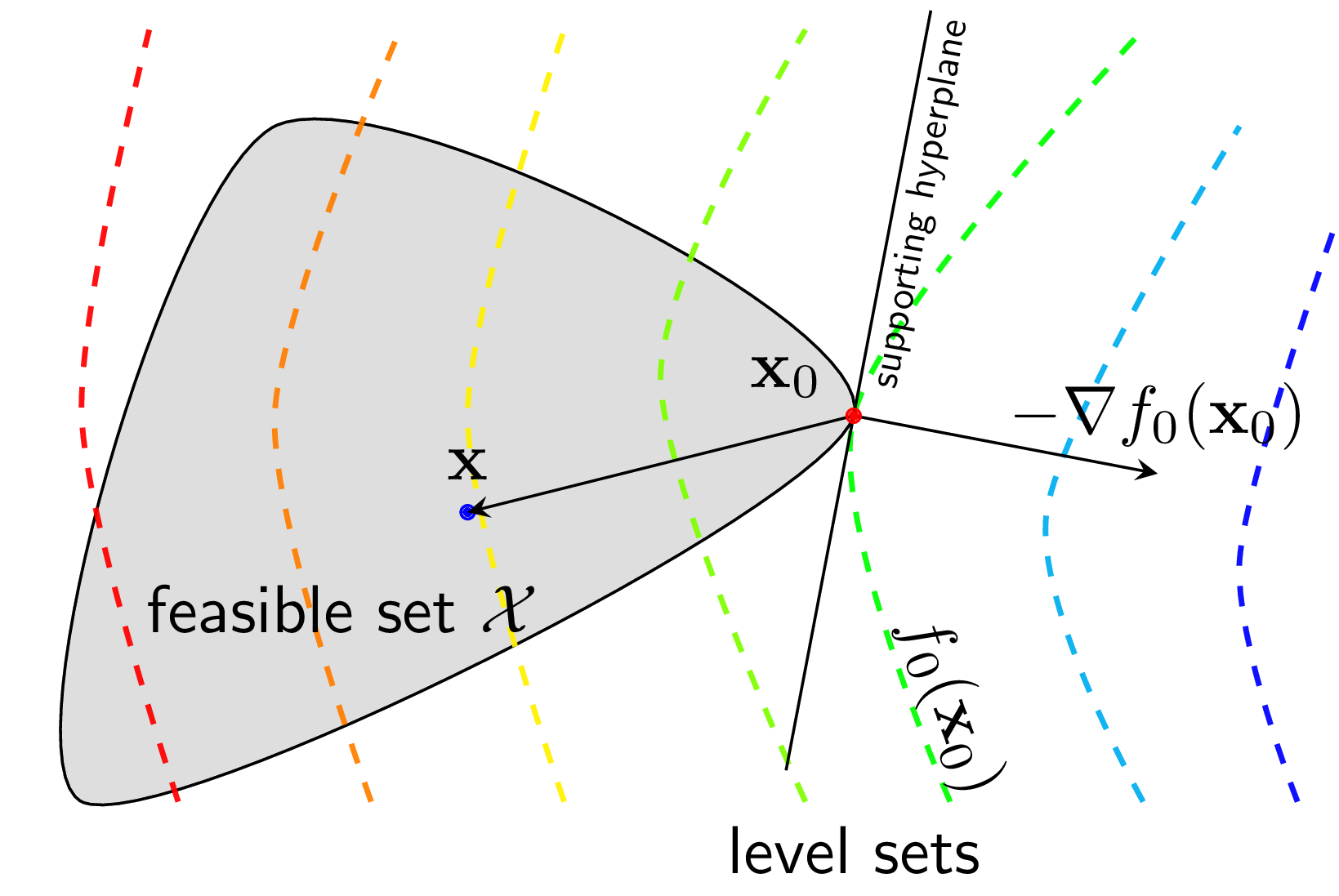
Mathematical Formulation

Standard Form:
minimize    f(x)
subject to  gᵢ(x) ≤ 0,  i = 1,...,m
            hⱼ(x) = 0,  j = 1,...,p

where f and gᵢ are convex, hⱼ are affine

Key Properties:
• Local minimum = Global minimum
• Efficient algorithms (polynomial time)
• Gradient descent converges

Code Example

from scipy.optimize import minimize
import numpy as np

# Example: Least Squares (convex)
# minimize ||Ax - b||²

# Generate problem data
np.random.seed(42)
A = np.random.randn(20, 10)
b = np.random.randn(20)

# Define objective and gradient
def objective(x):
    residual = A @ x - b
    return 0.5 * np.sum(residual**2)

def gradient(x):
    return A.T @ (A @ x - b)

# Solve
result = minimize(objective, x0=np.zeros(10), 
                 jac=gradient, method='BFGS')

print(f"Optimal value: {result.fun:.4f}")
print(f"Solution norm: {np.linalg.norm(result.x):.4f}")

# Compare with closed-form solution
x_optimal = np.linalg.lstsq(A, b, rcond=None)[0]
print(f"Closed-form solution norm: {np.linalg.norm(x_optimal):.4f}")

Convex Sets & Functions

Duality